Les mathématiques de Dieu ou la suite de Fibonacci

La suite de Fibonacci est une suite de nombres entiers dans laquelle chaque terme est la somme des deux termes précédents. Voici la suite de Fibonacci : 0, 1, 1, 2, 3, 5, 8, 13, 21, etc. Par exemple le chiffre 13 s’obtient en additionnant le chiffre 5 et 8. Le 21 en additionnant 8 et 13 et ainsi de suite.

Vous vous demandez peut-être pourquoi cette séquence de nombres est si célèbre ?

Et bien en fait, la séquence de Fibonacci est si célèbre car les scientifiques se sont rendus compte qu’elle fait partie intégrante de la nature. En effet, cette suite de nombres permet de créer une spirale logarithmique connue sous le nom de spirale de Fibonacci.

Et devinez quoi ? On la retrouve un peu partout… Des plus petits éléments de la nature aux objets les plus gigantesques. On retrouvera donc la spirale de Fibonacci dans les galaxies, l’ADN, les oeufs, les plantes, etc.

Voyant que l’univers répond à des lois mathématiques, la question qui se pose alors est… qui ou quoi a bien pu créer l’univers d’une manière si précise ?

En attendant d’avoir la réponse à cette question, nous vous laissons découvrir la spirale de Fibonacci au coeur de la nature…

Avant tout, voici comment obtenir la spirale de Fibonacci d’après la suite mathématique. On positionne simplement les nombres de la suite de Fibonacci de cette façon avant de tracer la spirale :

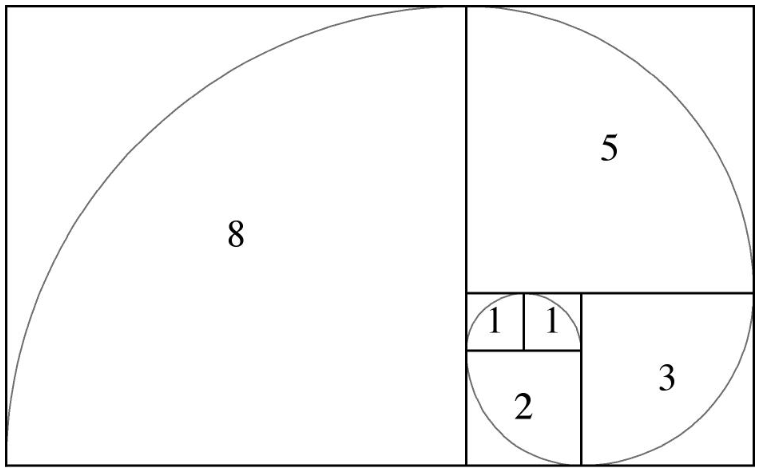
A partir de maintenant tenez-vous bien, nous partons à la découverte de la spirale de Fibonacci dans la nature…

On retrouvera alors cette spirale dans la coquille parfaite du Nautile…

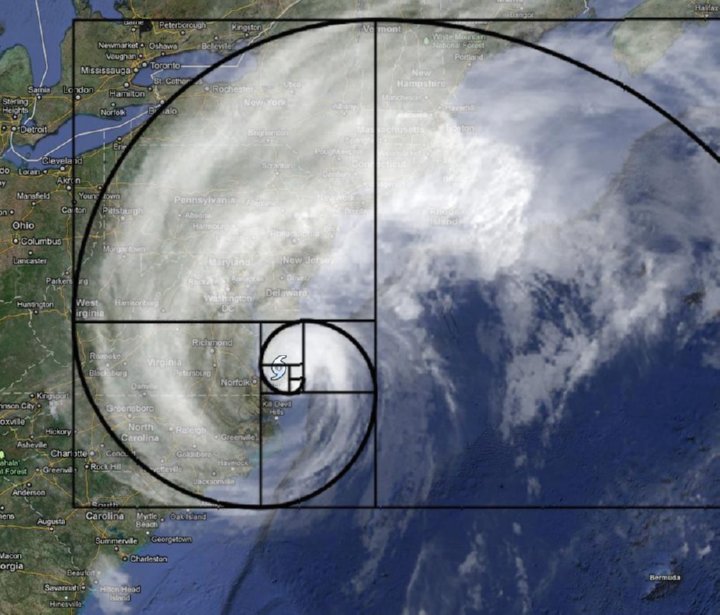
Ou encore dans la forme de l’Ouragan Irène…

Ou même dans la forme des galaxies en mouvement :

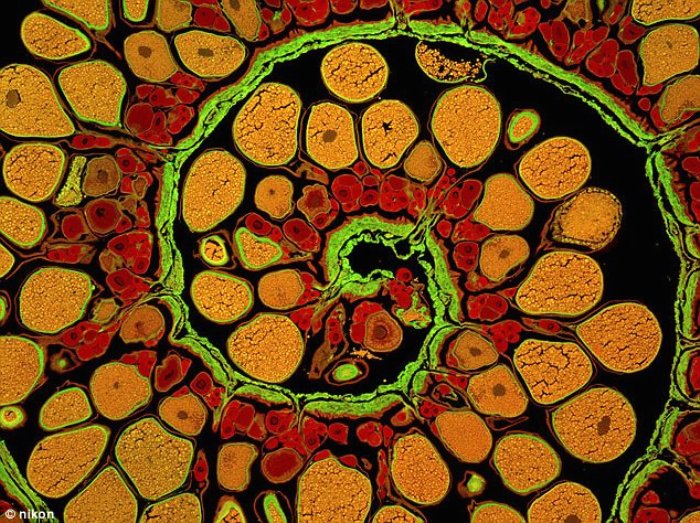
Ici, une vue microscopique de l’ovaire d’un poisson (la lotte de mer) :

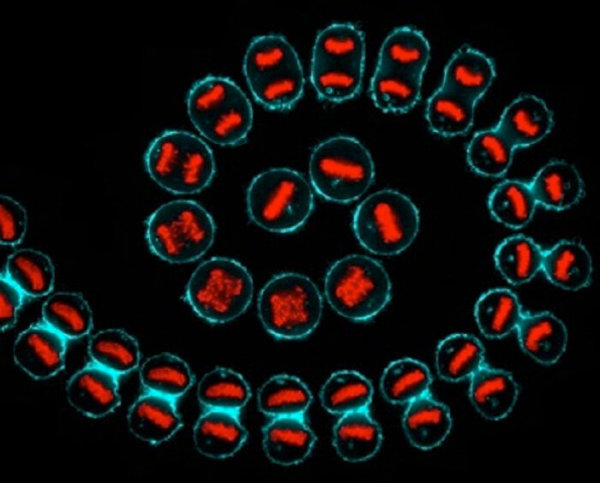
Ou dans la division d’une cellule cancéreuse. Cette micrographie confocale composite utilise la microscopie time-lapse pour montrer une cellule cancéreuse subissant une division cellulaire. L’ADN apparaît en rouge et la membrane cellulaire en cyan. La cellule ronde au centre a un diamètre de 20 microns :

Voici 16 autres exemples étonnants de la séquence de Fibonacci dans la nature

1 – Oeuf de poule

La suite de Fibonacci au début de la vie.

2 – Chou Romanesco

Le chou romanesco est un exemple frappant de la spirale de Fibonacci. Chaque nœud est une spirale de Fibonacci qui lui est propre.

3 – Aloe Vera

De nombreux cactus arborent la spirale de Fibonacci. Vous pouvez voir comment chaque ensemble de feuilles s’enroule en spirale.

4 – Buena Mulata

Le Buena Mulata est un piment qui lui aussi grandit selon la spirale de Fibonacci.

5 – La fleur de Tournesol

Ici aussi les graines de tournesol suivent, sur différents niveaux la spirale de Fibonacci. C’est un peu plus difficile à reconnaitre mais si vous regardez bien vous verrez que ce sont plusieurs spirales superposées avec un même point d’origine (le centre de la fleur).

6 – Les marguerites

Pareil que pour la fleur de Tournesol, ici on retrouve encore et toujours la spirale de Fibonacci.

7 – Les pommes de pin

Toutes les pommes de pin sont disposées et construites selon la séquence Fibonacci. La taille des cônes sur les pommes de pin augmente à mesure que vous vous déplacez vers l’extérieur en suivant encore et toujours la séquence de Fibonacci.

8 – Les caméléons

La queue de ces animaux s’enroule naturellement selon la spirale de Fibonacci.

9 – Mille-pattes géants d’Amérique

La spirale de Fibonacci est considérée comme le modèle de moindre résistance.

10 – Les chenilles

Une chenille monarque sur le point de former une chrysalide prend naturellement la forme d’une spirale de Fibonacci.

11 – Les pangolins

Au repos, les Pangolins aux écailles protectrices prennent la forme d’une spirale de Fibonacci afin de se reposer tout en protégeant leur ventre (partie molle qui ne contient aucune protection).

12 – Les fougères

Encore la spirale de Fibonacci dans les spores d’une fougère appelée Koru.

13 – Escargots et empreintes digitales

Ici, on peut retrouver la spirale de Fibonacci dans la forme de la coquille d’un escargot ainsi que des empreintes digitales.

14 – Les éléphants

Spirale de Fibonacci naturelle provenant de la trompe d’un éléphant jouant avec l’eau du fleuve.

15 – Les plantes

Encore une fois, la spirale de Fibonacci dans la formation des feuilles de fougères.

16 – Les oeuvres d’art

La spirale de Fibonacci dans l’oeuvre de Katsushika Hokusai : «La grande vague au large de Kanagawa». Il semble que même les oeuvres d’art ne puissent échapper à la séquence de Fibonacci.

Qui était Fibonacci ?

La séquence de Fibonacci doit son nom à Léonard de Pise, connu sous le nom de Fibonacci. Bien que Fibonacci ait introduit cette séquence dans le monde occidental pour la première fois en 1202, les mathématiciens indiens l’avaient déjà remarquée dès le sixième siècle apr. J.-C.

La suite de Fibonacci permet d’expliquer comment sont disposés les branches et les cernes de croissance d’un arbre, la disposition des feuilles sur une tige et la manière dont les écailles d’une pomme de pin sont placées.

Et pourtant, vous ne verrez pas la suite de Fibonacci partout car la nature fait preuve de créativité et de nuances afin de créer toute cette diversité.

Si vous désirez en savoir plus, voici les meilleurs livres sur la suite de Fibonacci :

• Comprendre le nombre d’or: sans les mathématiques, ou comment l’univers fonctionne en harmonie, le nombre d’or dans la grande pyramide de Gizeh de Jacques Grimault. Pour information, Jacques Grimault est l’informateur “caché” du documentaire Le secret des pyramides révélé.
• Le Nombre d’or: Les clés du mystère de Mario Livio
• Dieu est-il mathématicien ? de Mario Livio
• Le nombre d’Or : L’un des plus grands secrets de la nature de Scott Olsen
• The Fabulous Fibonacci Numbers de Alfred Posamentier and Ingmar Lehmann (Anglais seulement)
• Blockhead: The Life of Fibonacci de Joseph D’Agnese and John O’Brien (Anglais seulement)

Voici également 3 vidéos qui vous en diront plus sur la suite de Fibonacci :

Pour voir la vidéo avec les sous-titres en Français cliquez sur la petite roue, puis “auto-translate”, choisissez français et cliquez sur le bouton CC”

Voici maintenant une vidéo qui est plus “centrée sur les mathématiques”. Allergiques aux maths s’abstenir:

Pour avoir la vidéo avec les sous-titres en Français cliquez sur la petite roue, puis “auto-translate”, choisissez français et cliquez sur le bouton CC”

Maintenant enfin, voici une superbe petite vidéo de la chaîne YouTube “Spirit Science” qui décrit plus en détail les schémas de la vie et les mathématiques de Dieu :

Pour avoir la vidéo avec les sous-titres en Français cliquez sur la petite roue, puis “auto-translate”, choisissez français et cliquez sur le bouton CC”

Et vous qu’en pensez-vous ? Cette spirale de Fibonacci est-elle un pur hasard selon vous, ou est l’oeuvre d’un architecte ? N’hésitez pas à commenter juste en dessous ! 🙂